Sunday, January 10, 2016

Proof Cauchy Riemann Equations

Cauchy Riemann equations are necessary conditions but not sufficient conditions to check if a function is analytic or not. According to the definition of derivative we have
f'(z_0)=\lim\limits_{\Delta z\to 0}\dfrac{f(z_0+\Delta z)-f(z_0)}{\Delta z}
One important fact to take notice is 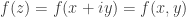f(z)=f(x+iy)=f(x,y)
\Rightarrow f'(z_0)=\lim\limits_{\Delta x+i \Delta y \to 0}\dfrac{f(z_0+\Delta z)-f(z_0)}{\Delta x+ i\Delta y}
For the derivative to exists at point 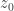z_0 it should be same no matter what path we take to reach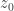 z_0
\Rightarrow f'(z_0)=\lim\limits_{x_0\to 0}\dfrac{f(z_0+\Delta z)-f(z_0)}{\Delta x}
Lets go around only x axis which means 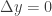\Delta y=0
\Rightarrow f'(x_0,y_0)=\lim\limits_{\Delta x \to 0}\dfrac{f(x_0+\Delta x,y_0)-f(x_0,y_0)}{\Delta x}
\Rightarrow f'(x_0,y_0)=\lim\limits_{\Delta x\to 0}\dfrac{u(x_0+\Delta x,y_0)+iv(x_0+\Delta x,y_0)-(u(x_0,y_0)+iv(x_0,y_0))}{\Delta x}
\Rightarrow f'(x_0,y_0)=\lim\limits_{\Delta x\to 0}\dfrac{u(x_0+\Delta x,y_0)-u(x_0,y_0)+iv(x_0+\Delta x,y_0)-iv(x_0,y_0)}{\Delta x}
\Rightarrow f'(x_0,y_0)=\lim\limits_{\Delta x\to 0}\dfrac{u(x_0+\Delta x,y_0)-u(x_0,y_0)}{\Delta x}+\lim\limits_{\Delta x\to 0}\dfrac{iv(x_0+\Delta x,y_0)-iv(x_0,y_0)}{\Delta x}
\Rightarrow f'(z_o)=u_x+iv_x
Now let’s go along only y axis i.e 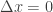\Delta x = 0
\Rightarrow f'(z_0)=\lim\limits_{\Delta y\to 0}\dfrac{f(z_0+\Delta z)-f(z_0)}{i\Delta y}
\Rightarrow f'(x_0+iy_0)=\lim\limits_{\Delta y\to 0}\dfrac{f(z_0+\Delta z)-f(z_0)}{i\Delta y}
\Rightarrow f'(x_0,y_0)=\lim\limits_{\Delta y \to 0}\dfrac{f(x_0,y_0+\Delta y)-f(x_0,y_0)}{i\Delta y}
\Rightarrow f'(x_0,y_0)=\lim\limits_{\Delta y\to 0}\dfrac{u(x_0,y_0+\Delta y)+iv(x_0,y_0+\Delta y)-(u(x_0,y_0)+iv(x_0,y_0))}{i\Delta y}
\Rightarrow f'(x_0,y_0)=\lim\limits_{\Delta y\to 0}\dfrac{u(x_0,y_0+\Delta y)-u(x_0,y_0)+iv(x_0,y_0+\Delta y)-iv(x_0,y_0)}{i\Delta y}
\Rightarrow f'(x_0,y_0)=\lim\limits_{\Delta y\to 0}\dfrac{u(x_0,y_0+\Delta y)-u(x_0,y_0)}{i\Delta y}+\lim\limits_{\Delta x\to 0}\dfrac{iv(x_0,y_0+\Delta y)-iv(x_0,y_0)}{i\Delta y}
\Rightarrow f'(x_0,y_0)=\lim\limits_{\Delta y\to 0}-i\dfrac{u(x_0,y_0+\Delta y)-u(x_0,y_0)}{\Delta y}+\lim\limits_{\Delta x\to 0}\dfrac{v(x_0,y_0+\Delta y)-v(x_0,y_0)}{\Delta y}
\Rightarrow f'(z_o)=-iu_y+v_y
\Rightarrow f'(z_o)=v_y-iu_y
Now if the derivative has to exist both of these should be same i.e
\Rightarrow f'(z_o)=u_x+iv_x=v_y-iu_y
Equating real and imaginary parts we get
\Rightarrow u_x=v_y and \Rightarrow u_y=-v_x

posted by Sumant at 8:32 PM 0 comments

-1/12

Let’s define three different series
S = 1+2+3+4+...
S_1 = 1-1+1-1+1-1+... =\frac{1}{2}
S_2 = 1-2+3-4+5-...
To find S_2 Let’s place a shifted copy of itself and add the corresponding terms 2S_2=S_2 +S_2 = (1-2+3-4+5-...)+(1-2+3-4+5-...)=1-1+1-1+1-1+.. = \frac{1}{2} \Rightarrow S_2= \frac{1}{4}
Now lets find S-S_2=(1+2+3+4+...)-(1-2+3-4+5-...)=(4+8+12+...)=4(1+2+3+...)=4S
\Rightarrow -S_2=3S
\Rightarrow -\frac{1}{4}=3S
\Rightarrow -\frac{1}{12}=S
The second proof also makes use of the idea we learned that
S_2 = 1-2+3-4+5-... =\frac{1}{4}
The way he goes to proof is using the idea of power series and differentiating it
\frac{1}{1-x}=1+x+x^2+x^3+...
Differentiating both sides we get
\frac{1}{(1-x)^2}=1+2x+3x^2+4x^3+5x^4+...
Now plug in -1 on both sides we get
\Rightarrow \frac{1}{4}=1-2+3-4+5-... and we have the same result.
The next thing he does is invoke the Reimann zeta function \zeta (s) = \frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+...
Notice that \zeta(-1) = 1+2+3+4+5+...
Now multiply both sides of \zeta(s) by \frac{2}{2^s} we get
\Rightarrow \zeta(s)\frac{2}{2^s}=\frac{2}{2^s}(\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+...)=(\frac{2}{2^s}+\frac{2}{4^s}+\frac{2}{6^s}+\frac{2}{8^s}+...)
Now subtracting this equation from the original \zeta(s) we get \Rightarrow \zeta(s)(1-\frac{2}{2^s})=\frac{1}{1^s}-\frac{1}{2^s}+\frac{1}{3^s}-\frac{1}{4^s}+...
Plugging back s= -1 we get
\Rightarrow \zeta(-1)(1-\frac{2}{2^{-1}}=1-2+3-4+5-6+...=\frac{1}{4}
\Rightarrow \zeta(-1)(-3)=\frac{1}{4}
\Rightarrow \zeta(-1)=\frac{-1}{12}
\Rightarrow 1+2+3+4+5+... =\frac{-1}{12}

posted by Sumant at 7:35 PM 0 comments

Site Meter