Proof Cauchy Riemann Equations
Cauchy Riemann equations are necessary conditions but not sufficient conditions to check if a function is analytic or not. According to the definition of derivative we have
One important fact to take notice is 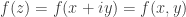
For the derivative to exists at point 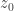 it should be same no matter what path we take to reach
it should be same no matter what path we take to reach 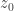
Lets go around only x axis which means 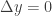
Now let’s go along only y axis i.e 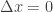
Now if the derivative has to exist both of these should be same i.e
Equating real and imaginary parts we get


0 Comments:
Post a Comment
<< Home