-1/12

Let’s define three different series

To find  Let’s place a shifted copy of itself and add the corresponding terms 

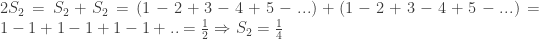
Now lets find 

The second proof also makes use of the idea we learned that

The way he goes to proof is using the idea of power series and differentiating it

Differentiating both sides we get

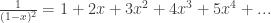
Now plug in  on both sides we get
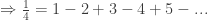 and we have the same result.
The next thing he does is invoke the Reimann zeta function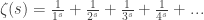 
Notice that 
Now multiply both sides of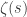  by 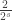 we get

Now subtracting this equation from the original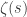  we get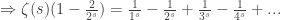 
Plugging back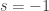  we get