Viete's Pi

as 

Plug  we get

Gammow's Problem

This is from the book One, Two infinity by George Gammow but I came across this in Paul Nahin’s “An Imaginary Tale”

A young and adventurous man who discovers an ancient parchment among his great grandfather’s paper listing about the great riches of golds and diamond necklaces he had stashed in an island up in the sea.

Sail to this island and you will find a deserted island. You will see two trees there. One is a Pine tree and other is an oak tree. There you will also see an old gallow on which we used to hang out traitors. Start from the gallow and walk to the oak tree counting your steps. At the oak tree you must turn right by a right angle and take the same number of steps. Put here a spike in the ground. Now you must return to the gallows and walk to the pine counting the steps. At the pine you must turn left by a right angle and take the same number of steps and put another spike into the ground. Dig halfway between the spikes; the treasure is there.

The young man follows the instructions, at least to the point of locating the island, where he sees the oak and pine trees. But, alas there is no gallow! Unlike the living trees, the gallows has long since disintegrated in the weather and not a trace of it or its location remains. Unable to carry out the rest of the instructions, the young man sails back without a gold coin or a diamond necklace to show for his troubles.

If he knew complex analysis he could have found the treasure.

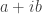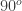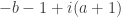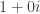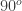To solve this let the coordinate of oak tree is -1 and pine tree is 1 on some scale. Let be the coordinate of the gallows. Then shifting the origin to oak  it becomes . Moving it by  it becomes . Shifting back we get . Now for the oak tree. We shift the origin to  it becomes rotating it by  in the clockwise direction is same as multiplying it by  we get . Shifting back to the origin this is 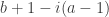. Now the treasure is buried between these two spikes.So the mid point is . Thus to find the treasure all he had to do was go the mid point between the two trees and then walk 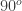 the same midway distance and dig there!

Mandelbrot Set using Sagemath

I generated this picture using Sagemath. Here is the code if you want to do the same

# Author: Sumant
# Design is to have the window size of -1 and 1 on x axis and -1 and 1 on y axis
# Parameter L controls number of points its for ex L = 10 means from -10 to 10 ie 20 pts
# So total of 20 times 20 = 400 pts will be used
# Dec-26-2015
z = var('z')
j=0
x=[] # Array to store 0 and 1 which is later changed to a matrix
X=70 # This is Precision choose from 10 and above, for 100 it takes around 1 minute 40 seconds to generate
Y=70
M=n(1/X) # For scaling the numbers
kX=range(-3*X,n(X/2)) #3 parts of negative x axis and 1/2 part of positive x axis
kY=range(-Y,Y)
def f(c):
    z=0 # Recall Mandebrot set always begins with zero
    for i in range(80): #This number calculates the number of iterations we have to do until it it exceeds 2
       z = z^2+c # This is the Mandelbrot set z = z^2+c, we start with
       if n(abs(z)) > 2:
            break
 
    if abs(z) > 2:
        return 0
    else:
        return 1

for i in kX:
    for j in kY:
        x.append(f((M*i+M*j*I)))# Populating the array

B=matrix(ZZ,3.5*X,x)# 3.5 is to compensate 3 parts of negative x axis and 1/2 part of positive x axis
matrix_plot(B.transpose())# Plotting the transpose image

Cauchy's Integral Formula

f  is a simple closed contour and if  is analystic on and inside of  then

Evaluate the following four integrals

Integrating using Complex numbers

The traditional method to integrate these functions is through integration by parts. However by using complex numbers one can integrate them even faster. $\int e^{ax}(\cos(bx)dx+i\int e^{ax}\sin(bx))dx$ $\int e^{ax}(\cos(bx)+i\sin(bx))dx$ $\Rightarrow \int e^{ax}e^{ibx}dx$ $\Rightarrow \int e^{(a+ib)x}dx$ $\Rightarrow \frac{e^{(a+ib)x}}{a+ib}+C$ $\Rightarrow \frac{e^{ax}e^{ibx}(a-ib)}{a^2+b^2}+C$ $\Rightarrow \frac{e^{ax}(\cos(bx)+i\sin(bx))(a-ib)}{a^2+b^2}+C$ $\Rightarrow \frac{e^{ax}(a\cos(bx)+b\sin(bx)+i(a\sin(bx)-b\cos(bx)))}{a^2+b^2}+C$ $\Rightarrow \frac{e^{ax}(a\cos(bx)+b\sin(bx))}{a^2+b^2}+i\frac{e^{ax}(a\sin(bx)-b\cos(bx))}{a^2+b^2}+C$ Thus $\int e^{ax}\cos(bx)dx=\frac{e^{ax}(a\cos(bx)+b\sin(bx))}{a^2+b^2}+C$ and $\int e^{ax}\sin(bx)dx=\frac{e^{ax}(a\sin(bx)-b\cos(bx))}{a^2+b^2}+C$

Easy mistake in proof by contradiction

Suppose we have to prove that $\sqrt{2}+\sqrt{6} < \sqrt{15}$. Now most people would do this way $(\sqrt{2}+\sqrt{6})^2 < (\sqrt{15})^2$ $\Rightarrow 2+6+2\sqrt{2}\sqrt{6} <15$ $\Rightarrow 2\sqrt{12} <7$ $\Rightarrow 48 <49$ However this is not the correct proof because $p \Rightarrow q$ is true even if $latex p$ is false. Therefore the correct way to do this will be let $\sqrt{2}+\sqrt{6} \ge \sqrt{15}$ $\Rightarrow (\sqrt{2}+\sqrt{6})^2 \ge (\sqrt{15})^2$ $\Rightarrow 2+6+2\sqrt{2}\sqrt{6} \ge 15$ $\Rightarrow 2\sqrt{12} \ge 7$ $\Rightarrow 48 \ge 49$ which is false. Hence we proved it by method of proof by contradiction

Del Ferro's depressed cubic equation solution

Del Ferro was the first person to have solved a variant of the cubic equation. This derivation is from Paul Nahin's book Imaginary Tale

He solved the equation $x^3+px=q$, where $p,q \in R,p,q >0$. Then he substituted for $x=m+n$

$ \Rightarrow (m+n)^3+p(m+n)=q$

$\Rightarrow m^3+n^3+3m^2n+3mn^2+pm+pn=q$

$\Rightarrow m^3+n^3+m(3mn+p)+n(3mn+p)=q$

$\Rightarrow m^3+n^3+(m+n)(3mn+p)=q$

Now is the magic step he puts $m^3+n^3=q, 3mn+p=0$

$\Rightarrow n= \frac{-p}{3m}$

$\Rightarrow m^3+\left (\frac{-p}{3m} \right)^3=q$

$\Rightarrow m^3-\frac{p^3}{27m^3}=q$

$\Rightarrow m^6-qm^3-\frac{p^3}{27m^3}=0$

As this is a quadratic equation in $ m^3$ by using the formula we get

$\Rightarrow m^3= \dfrac{q\pm \sqrt{q^2+\frac{4p^3}{27}}}{2}$

$\Rightarrow m^3= \dfrac{q\pm 2\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}{2}$

$\Rightarrow m^3= \frac{q}{2} \pm \sqrt{\frac{q^2}{4}+\frac{p^3}{27}}$

Taking positive first for $m^3$ we get

$\frac{q}{2} + \sqrt{\frac{q^2}{4}+\frac{p^3}{27}} +n^3=q$

$\Rightarrow n^3 =\frac{q}{2} - \sqrt{\frac{q^2}{4}+\frac{p^3}{27}}$

Hence we have $m =\sqrt[3]{\frac{q}{2}+ \sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$ and $n =\sqrt[3]{\frac{q}{2}- \sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$

$\Rightarrow x=\sqrt[3]{\frac{q}{2}+ \sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}+\sqrt[3]{\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}$

Polya's error problem

This is a problem I found in the preface of Dueling Idiots book. The problem is if Person A can detect "a" errors and Person B can detect "b" errors independent of other person and in common they detect "c" errors. What are the number of errors they missed.

Let there are "n" errors in total. $P(A) = \frac{a}{n}, P(B)=\frac{b}{n}$ then $P(A \cap B)= P(A) \times P(B)=\frac{a}{n}\times \frac{b}{n}= \frac{ab}{n^2}$. Since they have "c" errors in common which means $P(A \cap B)= \frac{c}{n}$. From these two equations we get $latex \frac{ab}{n^2}=\frac{c}{n} \Rightarrow n=\frac{ab}{c}$. Thus number of errors that are not found by both are $n -(a+b-c) = \frac{ab}{c}-(a+b-c)=\frac{ab-(ac+bc-c^2)}{c}=\frac{ab-ac-bc+c^2}{c}=\frac{a(b-c)-c(b-c)}{c}=\frac{(a-c)(b-c)}{c}$

Fast multiplication of two digits by 9!

I came across this trick in this video

It's a neat way to multiply by nine when the ten's digit is smaller than unit's digit for example like 23,,27, 38 and so on but not for 32,72,or 83. So how does it work.

So lets multiply $47 \times 9$

1. Write the first digit --> 4
2. how many digits in between the two digits --> 2  {5,6}
3. number of digits to make last digit reach 10--> 3 {8,9,10}

Therefore $l 47 \times 9=423$

Another quick example $ 29 \times 9 = 261$