Gammow's Problem

This is from the book One, Two infinity by George Gammow but I came across this in Paul Nahin’s “An Imaginary Tale”

A young and adventurous man who discovers an ancient parchment among his great grandfather’s paper listing about the great riches of golds and diamond necklaces he had stashed in an island up in the sea.

Sail to this island and you will find a deserted island. You will see two trees there. One is a Pine tree and other is an oak tree. There you will also see an old gallow on which we used to hang out traitors. Start from the gallow and walk to the oak tree counting your steps. At the oak tree you must turn right by a right angle and take the same number of steps. Put here a spike in the ground. Now you must return to the gallows and walk to the pine counting the steps. At the pine you must turn left by a right angle and take the same number of steps and put another spike into the ground. Dig halfway between the spikes; the treasure is there.

The young man follows the instructions, at least to the point of locating the island, where he sees the oak and pine trees. But, alas there is no gallow! Unlike the living trees, the gallows has long since disintegrated in the weather and not a trace of it or its location remains. Unable to carry out the rest of the instructions, the young man sails back without a gold coin or a diamond necklace to show for his troubles.

If he knew complex analysis he could have found the treasure.

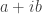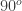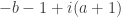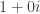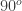To solve this let the coordinate of oak tree is -1 and pine tree is 1 on some scale. Let be the coordinate of the gallows. Then shifting the origin to oak  it becomes . Moving it by  it becomes . Shifting back we get . Now for the oak tree. We shift the origin to  it becomes rotating it by  in the clockwise direction is same as multiplying it by  we get . Shifting back to the origin this is 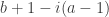. Now the treasure is buried between these two spikes.So the mid point is . Thus to find the treasure all he had to do was go the mid point between the two trees and then walk 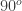 the same midway distance and dig there!